跟王小美与三岁一起学paddle — 卷积神经网络篇！

简单有趣带你深度学习

跟王小美与三岁一起学paddle 第四讲

致读者

在看这个notebook的你，对没错就是你

关注王小美喵，点个star⭐谢谢喵

注:本项目部分图片为自制，非授权请勿私自使用

王小美:

三岁老师，接下来是不是就要教我目标检测了呀？我已经准备好打穿csgo了 ٩(◕‿◕｡)۶

三岁:

可以是可以，但是千万别把号玩封了啊，那我们就马上来打开新大门—-卷积神经网络

首先我们要从卷积学起来哦！(～o￣3￣)～

卷积
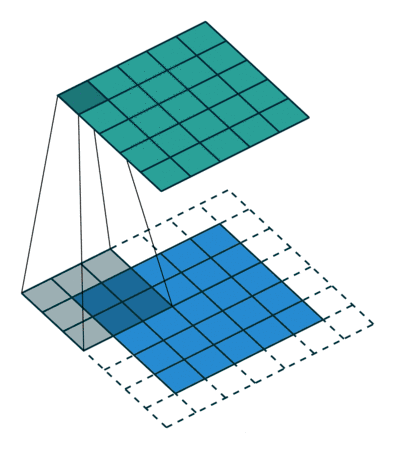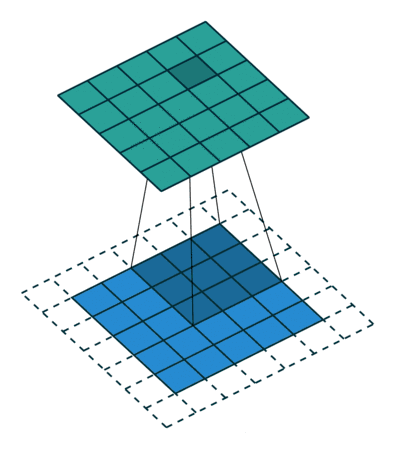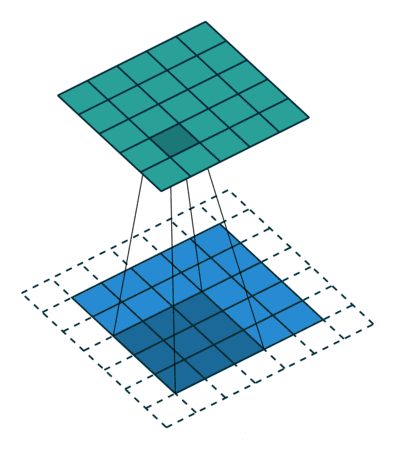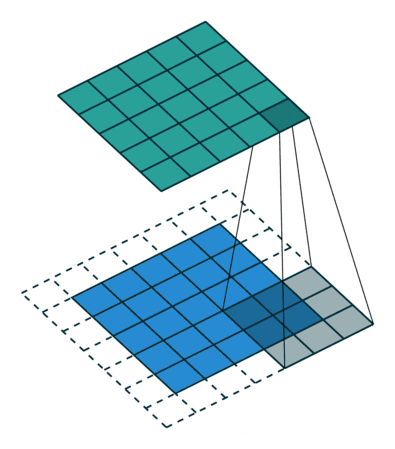
卷积运算是指从图像的左上角开始，开一个与模板同样大小的活动窗口，窗口图像与模板像元对应起来相乘再相加，并用计算结果代替窗口中心的像元亮度值。然后，活动窗口

向右移动一列，并作同样的运算。以此类推，从左到右、从上到下，即可得到一幅新图像。

我们也可以把卷积运算称之为滤波

王小美:

为什么要对图片进行卷积运算呢？｡◕ᴗ◕｡

三岁:

对于我们之前学的神经网络来说

一张图片所具有的信息量是非常大的，会有非常多的特征

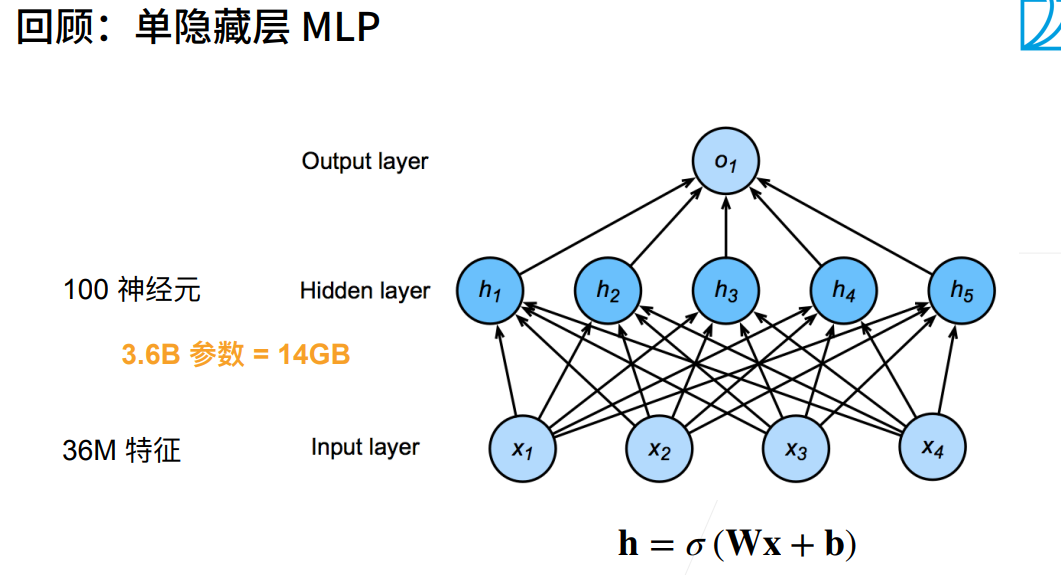
假设我们用一台1200w像素的手机拍摄图片将他传入单隐藏层的神经网络就需要14G的显存，何况我们还要多层呢？

所以我们必须对他进行处理，提取重要信息

三岁:

对图像滤波要遵从两个原则

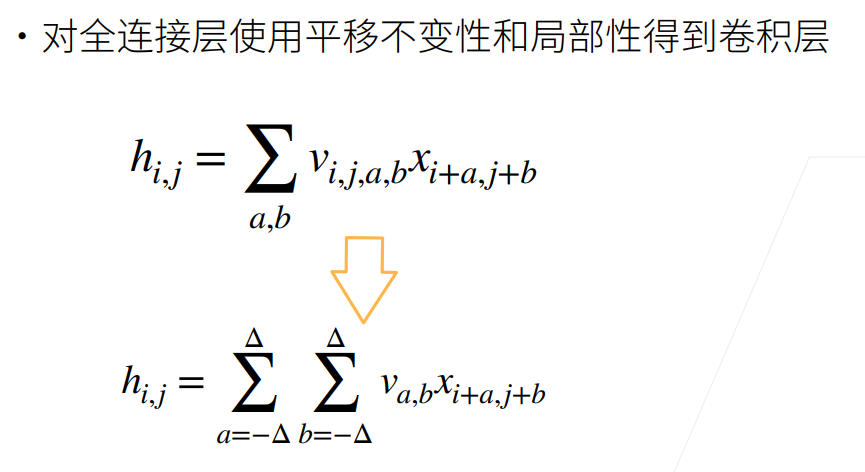
1.平移不变性

你找一个物品，不能受他位置的因素影响

2.局部性

你找一个物品，只需要在局部空间寻找

人们为了满足以上原则，使用了卷积

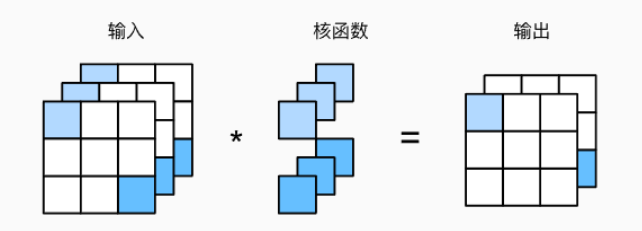
卷积层
将输入和卷积核进行交叉相关再加上偏置进行输出的层(对输入进行卷积运算的层)

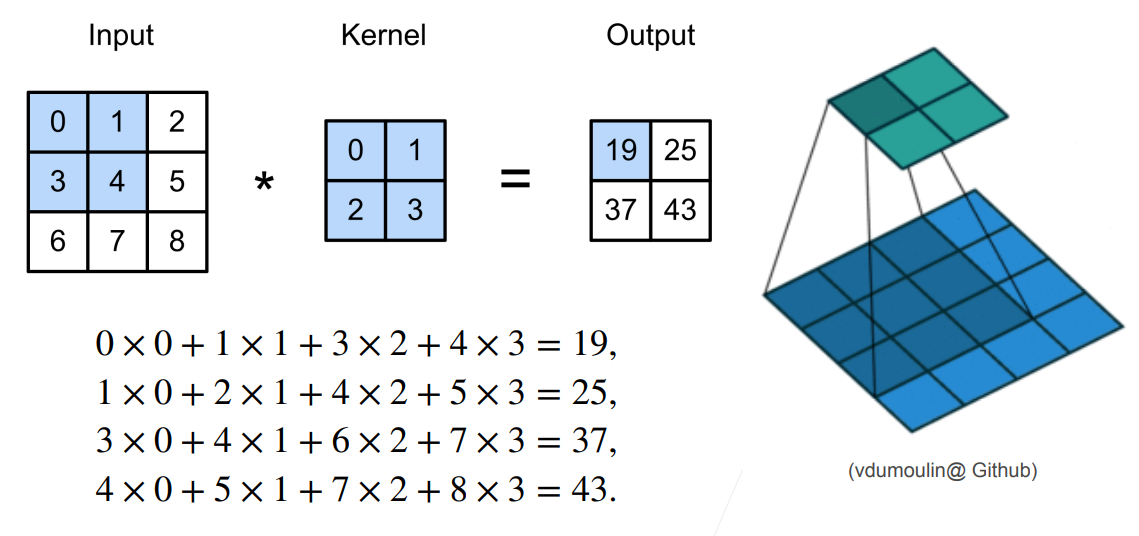
让我们来手动进行一次卷积吧！░ ∗ ◕ ں ◕ ∗ ░(下面这个例子我的偏置为0)

三岁:

在上图中，卷积核(Kernel)类似于线性回归的权重(W)

王小美:

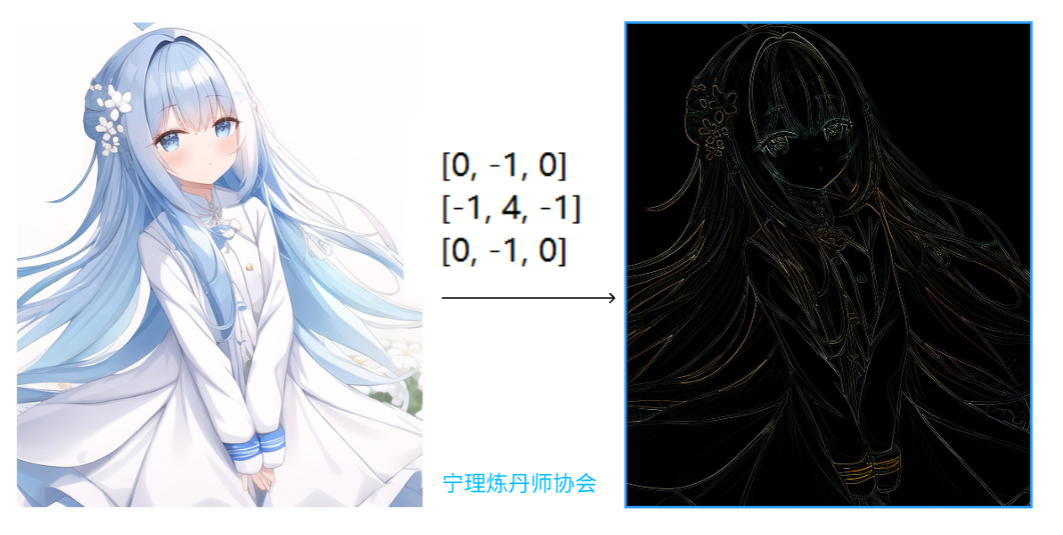
我对自己做了个卷积运算，大家快来看看吧！(o°ω°o)

不同的卷积核可以带来不同的效果哦，自己动手试试看吧

刚学习的小白可以使用啥都生大佬的图像增强工具

三岁:

假设原图像的高为H 宽为W

卷积核的高为Kh，宽为Kw

当我们对图像做卷积的时候，我们发现输出图像的高是(H-Kh+1)，宽是(W-Kw+1)

我们会发现，通过卷积输出的图像是越来越小的，并且如果卷积核越大，输出的图像就越小，如果我们输入的图像比较小的时候这就不利于我们搭建多层网络了。

那么我们要如何对输入图像做处理呢？

王小美:

无敌的王小美出现了，并说了一句：把输入图像变大就行了。 o(>ω<)o

三岁:

填充(padding)
是的，在输入图像周围填充空白像素，这个操作我们叫做padding(填充)

假设我们填充Pw，Ph

那么输出图像的长是(W-Kw+Pw+1) 宽是(H-Kh+Ph+1)

当Pw = Kw-1， Ph = Kh-1 输出图像大小就与输入图像大小一样了

当Kw是奇数时 Pw为偶数我们会在上下左右padding P/2

当Kw是偶数时，Pw为奇数，我们会padding 向上取整P/2(这个情况非常少见)

三岁:

当我们输入的图像比较大，但是在深度学习中我们一般采用的卷积核是比较小的，我们就需要特别多的层才能把图像大小降下来，
大家知道层数越多计算就越复杂，我们不希望这样的情况发生

王小美:

这时候就要让卷积核迈大脚步了 o(>ω<)o

三岁:

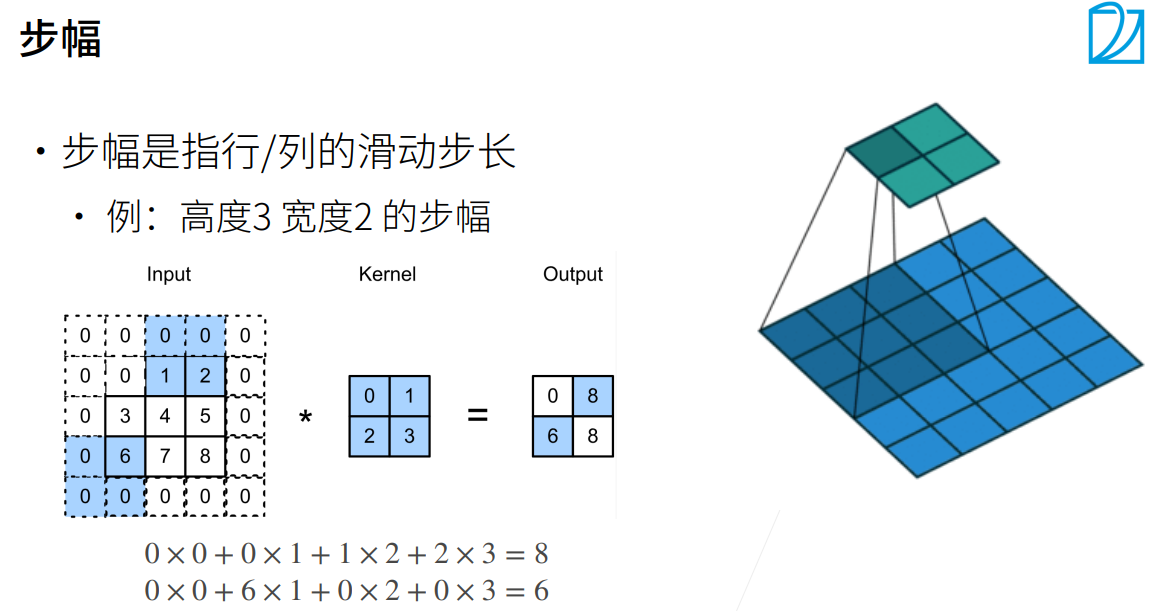
步幅(Stride)
卷积过程中，有时需要通过填充来避免信息损失，有时也要在卷积时通过设置的步长(Stride)来压缩一部分信息。因此卷积中的步幅是另一个构建卷积神经网络的基本操作。

例如下图

三岁:

这里补充一下通过卷积后输出的大小的计算公式

多通道的输入和输出

我们都知道图片是彩色的，一般来说图片有RGB三个通道

下面有请今天的玩伴女郎 — Lena同学！！！ ๑乛◡乛๑

为了直观显示，我把单个通道的亮度分别调到255

然后我们把三个通道的图片输入到网络中。不过我们要如何处理呢？

二维卷积

王小美:

我猜，刚刚一个输入用一个卷积核，现在有三个应该要用三个卷积核。(⊙ᗜ⊙)

三岁:

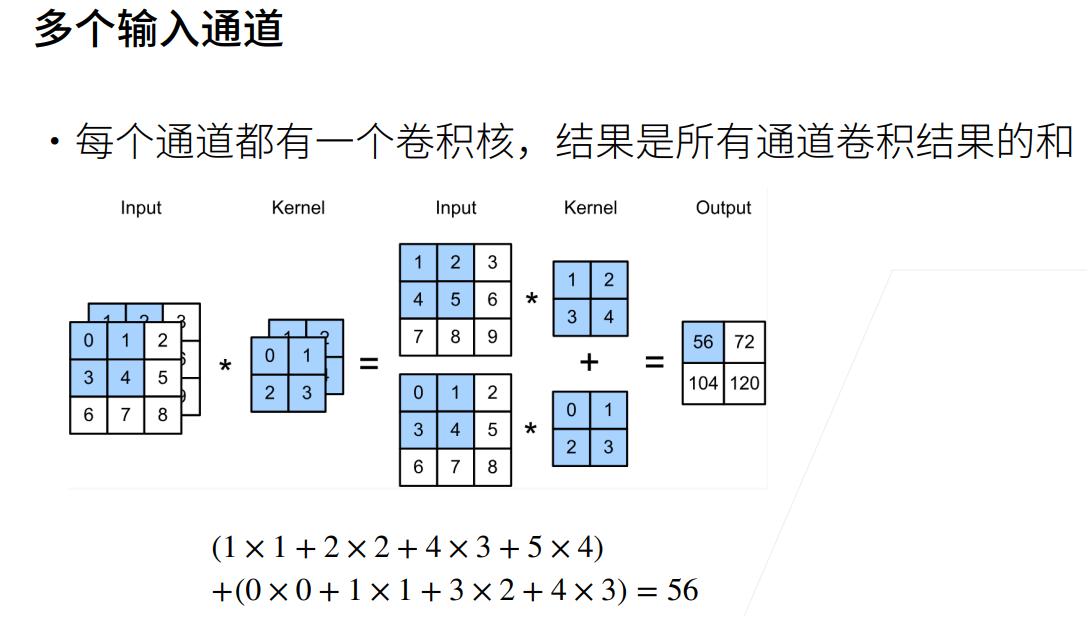
没错，我们将每个通道的图片和一个卷积核卷积，三个通道就有三个卷积后的输出，然后我们将输出矩阵相加就可以得到一个输出。这样的方式我们可以叫他二维卷积

让我们来看下具体过程吧！(以输入通道为2为例)｡◕ᴗ◕｡

三维卷积

王小美:

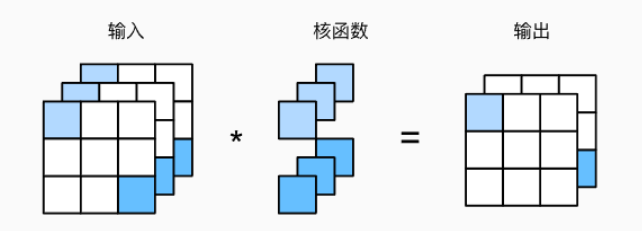
我懂了，三个卷积核可以有一个输出，如果我要多通道输出的话，我整多批的三个卷积核对输入图像卷积我就可以得到多个输出了！ᕙ( * •̀ ᗜ •́ * )ᕗ

三岁:

没错，这就是多输出的方法，我们也可以叫做三维卷积，可以看一下过程｡◕ᴗ◕｡

我们可以将每个通道看作是对不同特征的响应。而现实可能更为复杂一些，因为每个通道不是独立学习的，而是为了共同使用而优化的。因此，多输出通道并不仅是学习多个单通道的检测器。

三岁:

眼尖的同学是不是有一个疑问，为什么我上面图片中用到了一个1x1的卷积核

哈哈，这又是一个知识点了o(￣▽￣)ｄ

1×1 卷积层
先说我们为什么要引入一个1x1的卷积层，我们发现，这个卷积层并不会压缩大小，而是将三个通道的信息进行了整合变成了一个通道

因为使用了最小窗口，卷积失去了在高度和宽度维度上识别相邻元素间相互作用的能力，而是在通道上具有了能力我们可以将1x1卷积层看作是在每个像素位置应用了全连接层

因此1x1卷积层是一个受欢迎的选择

第一阶段小结
1.卷积是对图像提取特征的操作

2.填充能减少边缘信息丢失

3.如果我们发现原始的输入分辨率十分冗余我们可以增大步幅

4.输出通道数是卷积层的超参数

5.二维卷积: 每个输入通道有独立的二维卷积核，所有通道结果相加得到一个输出通道结果

6.三维卷积: 每个输出通道有独立的三维卷积核

汇聚层(池化层)
由于卷积层对位置信息特别的敏感，可能因为物体位置不同导致卷积无法很好的处理。

这个时候就需要用到池化层

池化层能保持一定范围内的不变性，削弱卷积层对位置的过度敏感性。

池化有很多种最大池化、平均池化、重叠池化、非重叠池化、金字塔池化SPP、双线性池化（Bilinear Pooling）

这里我主要讲最常用的最大池化和平均池化

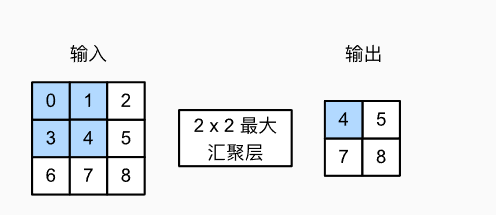
最大池化(Max-Pooling)

与卷积类似，最大池化也是以滑窗的方式进行，不过不同的是池化并没有用卷积核，而是算出跟窗口一样大的区域内的最大值。

池化和卷积一样也有填充和步幅

三岁:

让我们来看看池化是如何削弱卷积对位置信息的过度敏感

对输入图像先用左边是1右边是-1的2x2卷积核进行卷积，再对输出结果做最大池化，我们会发现出现了一个像素的位移，使得卷积核对位置的敏感度降低

平均池化(Mean-Pooling)

平均池化也是通过滑窗的方式，只不过将之前取最大的计算方式换成求平均

王小美:

这两种不同的池化有啥区别吗ヾ（≧?≦）〃？？

三岁:

一般来说，mean-pooling能减小第一种误差，更多的保留图像的背景信息，max-pooling能减小第二种误差，更多的保留纹理信息。

三岁:

好了，基本概念就讲到这了。让我们进入卷积神经网络吧！ o(>ω<)o

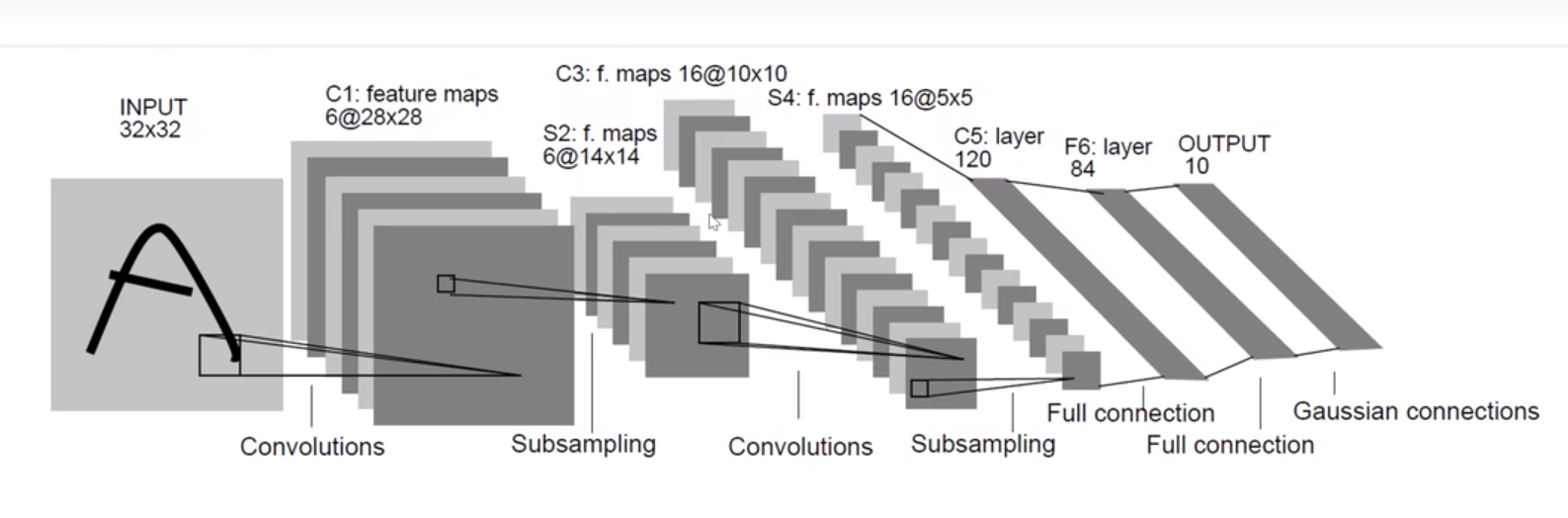
经典卷积神经网络 LeNet(卷积神经网络中的HelloWorld)

这个模型是由AT&T贝尔实验室的研究员Yann LeCun在1989年提出的（并以其命名），目的是识别图像LeCun.Bottou.Bengio.ea.1998中的手写数字。当时，Yann LeCun发表了第一篇通过反向传播成功训练卷积神经网络的研究，这项工作代表了十多年来神经网络研究开发的成果。

当时，LeNet取得了与支持向量机（SVM）性能相媲美的成果，成为监督学习的主流方法。 LeNet被广泛用于自动取款机（ATM）机中，帮助识别处理支票的数字。时至今日，一些自动取款机仍在运行Yann LeCun和他的同事Leon Bottou在上世纪90年代写的代码呢！

三岁:

通过这样图我们可以对Lenet网络的结构有很好的认识。接下来让我们通过paddle来复现一下Lenet吧！o(>ω<)o

回顾一下我们之前讲的softmax实现图像分类任务

为了能够应用softmax回归，我们首先将每个大小为28×28的图像使用paddle.nn.Flatten展平为一个784维的固定长度的一维向量，然后用全连接层对其进行处理。
这样的做法会丢失很多空间信息，而现在，我们已经掌握了卷积层的处理方法，我们可以在图像中保留空间结构

import paddle
from paddle import nn, optimizer

net = nn.Sequential(
    nn.Conv2D(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    # 一个输入6个输出 padding=2可以把28x28补到32x32，使用了sigmoid激活函数使其具有非线性性，
    # 关于激活函数的介绍我们下节课再讲，除了sigmoid你还可以是试试relu、tanh，relu是我们当今最常用的
    nn.AvgPool2D(kernel_size=2, stride=2),
    nn.Conv2D(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2D(kernel_size=2, stride=2),
    nn.Flatten(),
    # 由于后面要接全连接层所以这边将他摊平
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

# 由于Lenet后面接的高斯层我们当今已经不再使用了，所以这里就将其去除了。除此之外该网络与上图一致

W0113 17:24:16.045086   180 gpu_resources.cc:61] Please NOTE: device: 0, GPU Compute Capability: 7.0, Driver API Version: 11.2, Runtime API Version: 11.2
W0113 17:24:16.049470   180 gpu_resources.cc:91] device: 0, cuDNN Version: 8.2.

1 2	# 让我们来看一下网络情况 paddle.summary(net,(1, 1, 28, 28))

---------------------------------------------------------------------------
 Layer (type)       Input Shape          Output Shape         Param #    
===========================================================================
   Conv2D-1       [[1, 1, 28, 28]]      [1, 6, 28, 28]          156      
   Sigmoid-1      [[1, 6, 28, 28]]      [1, 6, 28, 28]           0       
  AvgPool2D-1     [[1, 6, 28, 28]]      [1, 6, 14, 14]           0       
   Conv2D-2       [[1, 6, 14, 14]]     [1, 16, 10, 10]         2,416     
   Sigmoid-2     [[1, 16, 10, 10]]     [1, 16, 10, 10]           0       
  AvgPool2D-2    [[1, 16, 10, 10]]      [1, 16, 5, 5]            0       
   Flatten-1      [[1, 16, 5, 5]]          [1, 400]              0       
   Linear-1          [[1, 400]]            [1, 120]           48,120     
   Sigmoid-3         [[1, 120]]            [1, 120]              0       
   Linear-2          [[1, 120]]            [1, 84]            10,164     
   Sigmoid-4         [[1, 84]]             [1, 84]               0       
   Linear-3          [[1, 84]]             [1, 10]              850      
===========================================================================
Total params: 61,706
Trainable params: 61,706
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.11
Params size (MB): 0.24
Estimated Total Size (MB): 0.35
---------------------------------------------------------------------------






{'total_params': 61706, 'trainable_params': 61706}

但是Sequential(循序容器)顾名思义，只能搭建循序执行的网络，一些跳跃连接的网络无法执行，所以可以用class创建一个类


class LeNet(nn.Layer):
    """
    继承paddle.nn.Layer定义网络结构
    """

    def __init__(self, num_classes=10):
        """
        初始化函数
        """
        super(LeNet, self).__init__()

        self.features = nn.Sequential(
            nn.Conv2D(in_channels=1, out_channels=6, kernel_size=3, stride=1, padding=1),  # 第一层卷积
            nn.Sigmoid(), # 激活函数
            nn.MaxPool2D(kernel_size=2, stride=2),  # 最大池化，下采样
            nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0), # 第二层卷积
            nn.Sigmoid(), # 激活函数
            nn.MaxPool2D(kernel_size=2, stride=2) # 最大池化，下采样
        )

        self.fc = nn.Sequential(
            nn.Linear(400, 120),  # 全连接
            nn.Linear(120, 84),   # 全连接
            nn.Linear(84, num_classes) # 输出层
        )

    def forward(self, inputs):
        """
        前向计算
        """
        y = self.features(inputs)
        y = paddle.flatten(y, 1)
        out = self.fc(y)

        return out

network_2 = LeNet()
paddle.summary(network_2,(1, 1, 28, 28))

---------------------------------------------------------------------------
 Layer (type)       Input Shape          Output Shape         Param #    
===========================================================================
   Conv2D-3       [[1, 1, 28, 28]]      [1, 6, 28, 28]          60       
   Sigmoid-5      [[1, 6, 28, 28]]      [1, 6, 28, 28]           0       
  MaxPool2D-1     [[1, 6, 28, 28]]      [1, 6, 14, 14]           0       
   Conv2D-4       [[1, 6, 14, 14]]     [1, 16, 10, 10]         2,416     
   Sigmoid-6     [[1, 16, 10, 10]]     [1, 16, 10, 10]           0       
  MaxPool2D-2    [[1, 16, 10, 10]]      [1, 16, 5, 5]            0       
   Linear-4          [[1, 400]]            [1, 120]           48,120     
   Linear-5          [[1, 120]]            [1, 84]            10,164     
   Linear-6          [[1, 84]]             [1, 10]              850      
===========================================================================
Total params: 61,610
Trainable params: 61,610
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.11
Params size (MB): 0.24
Estimated Total Size (MB): 0.35
---------------------------------------------------------------------------






{'total_params': 61610, 'trainable_params': 61610}

三岁:

让我们来试试模型的效果吧！

还记得我们的步骤吗？

1.数据处理

# 通过paddle2.0的数据集读取api读取数据
import paddle.vision.transforms as T
transform = T.Normalize(mean=[127.5], std=[127.5]) # 将数据归一化到[-1, 1]，参考原论文
train_dataset = paddle.vision.datasets.MNIST(mode='train', transform=transform)
val_dataset =  paddle.vision.datasets.MNIST(mode='test', transform=transform)
print("训练集有{}\n测试集有{}".format(len(train_dataset),len(val_dataset)))

item    8/2421 [..............................] - ETA: 8s - 4ms/item

Cache file /home/aistudio/.cache/paddle/dataset/mnist/train-images-idx3-ubyte.gz not found, downloading https://dataset.bj.bcebos.com/mnist/train-images-idx3-ubyte.gz 
Begin to download


item 8/8 [============================>.] - ETA: 0s - 5ms/item


Download finished
Cache file /home/aistudio/.cache/paddle/dataset/mnist/train-labels-idx1-ubyte.gz not found, downloading https://dataset.bj.bcebos.com/mnist/train-labels-idx1-ubyte.gz 
Begin to download

Download finished


item  12/403 [..............................] - ETA: 2s - 7ms/item

Cache file /home/aistudio/.cache/paddle/dataset/mnist/t10k-images-idx3-ubyte.gz not found, downloading https://dataset.bj.bcebos.com/mnist/t10k-images-idx3-ubyte.gz 
Begin to download


item 2/2 [===========================>..] - ETA: 0s - 3ms/item


Download finished
Cache file /home/aistudio/.cache/paddle/dataset/mnist/t10k-labels-idx1-ubyte.gz not found, downloading https://dataset.bj.bcebos.com/mnist/t10k-labels-idx1-ubyte.gz 
Begin to download

Download finished


训练集有60000
测试集有10000

# 使用matplotlib库绘制图像
import numpy as np
import matplotlib.pyplot as plt
print('图片：')
print(type(train_dataset[0][0]))
print(train_dataset[0][0].shape)
print('Label：')
print(type(train_dataset[0][1]))
print(train_dataset[0][1])

# 可视化展示
plt.figure()
plt.imshow(train_dataset[0][0].reshape([28,28]), cmap=plt.cm.binary)
plt.show()

图片：
<class 'numpy.ndarray'>
(1, 28, 28)
Label：
<class 'numpy.ndarray'>
[5]


/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/image.py:425: DeprecationWarning: np.asscalar(a) is deprecated since NumPy v1.16, use a.item() instead
  a_min = np.asscalar(a_min.astype(scaled_dtype))
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/image.py:426: DeprecationWarning: np.asscalar(a) is deprecated since NumPy v1.16, use a.item() instead
  a_max = np.asscalar(a_max.astype(scaled_dtype))

png

三岁:

还记得我们之前说的通过paddle api进行训练吗？ ٩(◕‿◕｡)۶

忘了的请务必再看一次，没点赞的话记得点个赞哈哈

不记得的话再看一次吧！点击跳转

2.组网

这里因为前面已经组好了所以直接跳下一步

3.训练和调参

model = paddle.Model(network_2)

# 模型配置
model.prepare(paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters()), # Adam优化器
              paddle.nn.CrossEntropyLoss(), # 损失函数 交叉熵
              paddle.metric.Accuracy()) # 评估指标

# 启动全流程训练
model.fit(train_dataset,  # 训练数据集
          val_dataset,   # 评估数据集
          epochs=5,       # 训练轮次
          batch_size=64,  # 单次计算数据样本量
          verbose=1)      # 日志展示形式，进度条

The loss value printed in the log is the current step, and the metric is the average value of previous steps.
Epoch 1/5
step 938/938 [==============================] - loss: 0.1858 - acc: 0.8464 - 10ms/step          
Eval begin...
step 157/157 [==============================] - loss: 0.0200 - acc: 0.9503 - 8ms/step          
Eval samples: 10000
Epoch 2/5
step 938/938 [==============================] - loss: 0.0871 - acc: 0.9550 - 10ms/step          
Eval begin...
step 157/157 [==============================] - loss: 0.0068 - acc: 0.9703 - 8ms/step          
Eval samples: 10000
Epoch 3/5
step 938/938 [==============================] - loss: 0.0128 - acc: 0.9667 - 10ms/step          
Eval begin...
step 157/157 [==============================] - loss: 0.0036 - acc: 0.9717 - 8ms/step          
Eval samples: 10000
Epoch 4/5
step 938/938 [==============================] - loss: 0.0079 - acc: 0.9720 - 10ms/step          
Eval begin...
step 157/157 [==============================] - loss: 0.0026 - acc: 0.9774 - 8ms/step          
Eval samples: 10000
Epoch 5/5
step 938/938 [==============================] - loss: 0.1188 - acc: 0.9763 - 9ms/step          
Eval begin...
step 157/157 [==============================] - loss: 4.6758e-04 - acc: 0.9826 - 8ms/step      
Eval samples: 10000

模型验证

1 2	# 用测试集进行测试 model.evaluate(val_dataset, verbose=1)

Eval begin...
step 10000/10000 [==============================] - loss: 3.5763e-07 - acc: 0.9826 - 2ms/step          
Eval samples: 10000





{'loss': [3.576278e-07], 'acc': 0.9826}

Model.predict
高层 API 中提供了 Model.predict 接口，可对训练好的模型进行推理验证。只需传入待执行推理验证的样本数据，即可计算并返回推理结果。

返回格式是一个列表：

模型是单一输出：[(numpy_ndarray_1, numpy_ndarray_2, …, numpy_ndarray_n)]

模型是多输出：[(numpy_ndarray_1, numpy_ndarray_2, …, numpy_ndarray_n), (numpy_ndarray_1, numpy_ndarray_2, …, numpy_ndarray_n), …]

如果模型是单一输出，则输出的形状为 [1, n]，n 表示数据集的样本数。其中每个 numpy_ndarray_n 是对应原始数据经过模型计算后得到的预测结果，类型为 numpy 数组，例如 mnist 分类任务中，每个 numpy_ndarray_n 是长度为 10 的 numpy 数组。

如果模型是多输出，则输出的形状为[m, n]，m 表示标签的种类数，在多标签分类任务中，m 会根据标签的数目而定。

1 2	# 批量预测测试集 result = model.predict(val_dataset)

Predict begin...
step 10000/10000 [==============================] - 2ms/step          
Predict samples: 10000

# 可视化结果

# 定义画图方法
def show_img(img, predict):
    plt.figure()
    plt.title('predict: {}'.format(predict))
    plt.imshow(img.reshape([28, 28]), cmap=plt.cm.binary)
    plt.show()

# 抽样展示
indexs = [2, 66, 33, 222]

for idx in indexs:
    show_img(val_dataset[idx][0], np.argmax(result[0][idx]))

# np.argmax是用于取得数组中每一行或者每一列的的最大值

png

4.模型保存与加载

1 2	# 保存模型 model.save('model/mnist')

# 加载动态图模型参数和优化器参数
model.load('/home/aistudio/model/mnist')
model.fit(train_dataset, epochs=2, batch_size=64, save_freq=1, verbose=1)

# 通过它的参数 save_freq可以设置保存动态图模型的频率，即多少个 epoch 保存一次模型，默认值是 1。

The loss value printed in the log is the current step, and the metric is the average value of previous steps.
Epoch 1/2
step 938/938 [==============================] - loss: 0.0201 - acc: 0.9788 - 10ms/step          
Epoch 2/2
step 938/938 [==============================] - loss: 0.0183 - acc: 0.9808 - 9ms/step

1 2	# 用测试集进行测试 model.evaluate(val_dataset, verbose=1)

Eval begin...
step 10000/10000 [==============================] - loss: 5.9605e-07 - acc: 0.9840 - 2ms/step          
Eval samples: 10000





{'loss': [5.960463e-07], 'acc': 0.984}